蔡司三坐標測量實操講解——最小二乘法擬合

坐標點擬合
坐標點數據需要經過計算機處理,擬合形成測量元素,比如直線、平面、圓、圓柱、圓錐等,再經過特定的數字計算方法得出其形狀、位置公差以及其他幾何量數據。
不太能理解?那我們舉個例子。
假設我們要測量一個圓柱體零件

首先,為了簡化問題難度我們將三維問題變為二維問題,只考慮XY坐標。在圓柱上任一截面,每間隔18°取一個測量點,一共取20個測量坐標點。并在X0Y坐標系里表示出來。
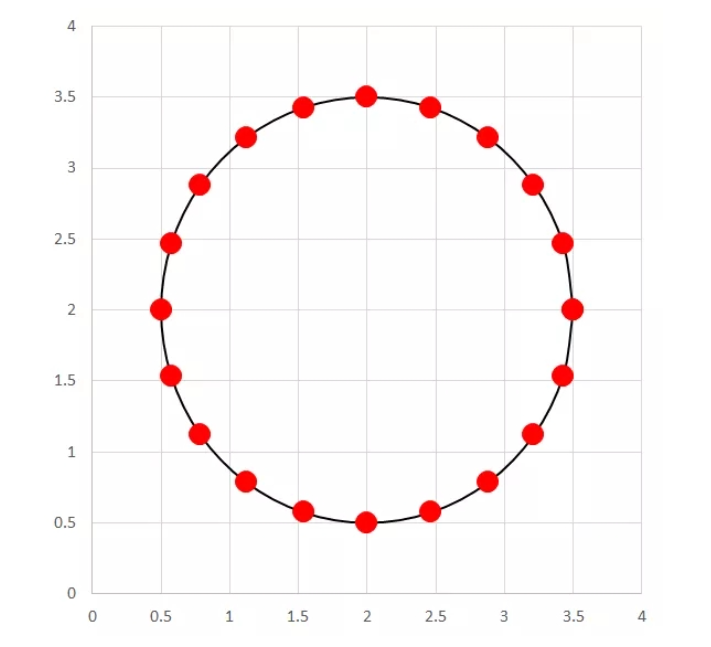
上面的圖看起來是一個圓,但是問題沒這么簡單。這個世界上有一種東西叫誤差,而誤差是絕對存在的。簡單來說,由于誤差的存在,實際存在的東西和理論形狀是有偏差的,比如說我們平時看到的平面,在微觀尺度下是這樣的:

同樣,由于機床本身的誤差外加裝夾誤差、加工熱誤差、振動誤差等原因。被加工圓實際上也不是理想圓,只是因為誤差本身數值很小,肉眼難以分辨。為了讓大家形象的觀察到誤差的存在,我們把剛才被測圓數據的誤差放大幾百倍,看似完美的圓就變成了下面的不規則多邊形:
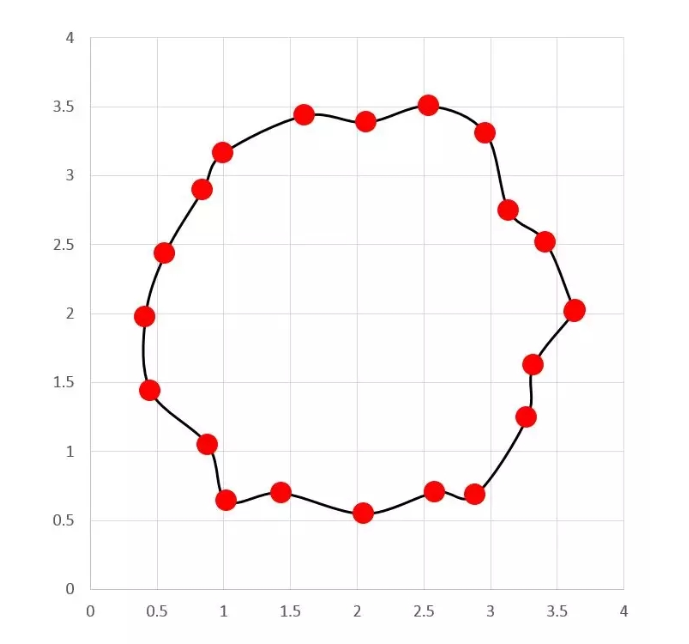
此時,我們不難看出,這些實測坐標點似乎不像一個圓。但是,它又的的確確是一個實際圓柱上的坐標值。那么問題來了:
它的直徑是多少?
它的圓心又在哪里?
此刻,我們需要找一個理想的圓來表示出這個實際上并不理想的圓,這個過程就是前面提到的坐標點擬合過程:
首先,我們假設有這樣一個理想圓的存在,如下圖:
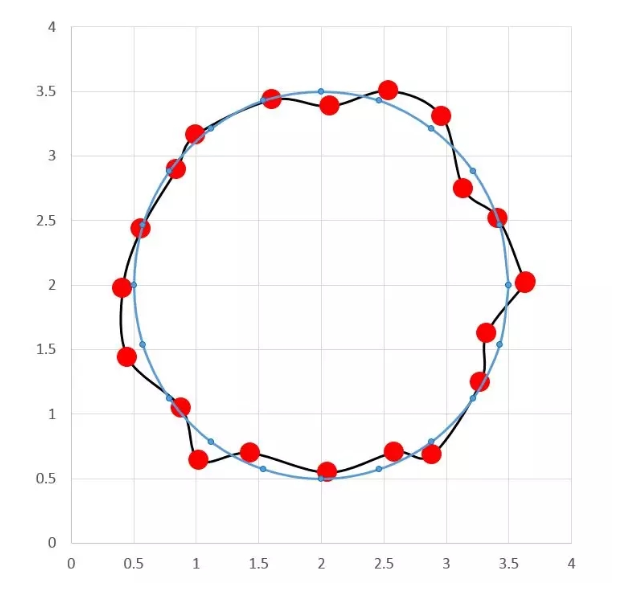
接下來我們分析一下這個理想圓存在的條件:
對比實際測量點與理想圓相應位置點(每間隔18°位置),他們之間的距離就是加工誤差,用黃色線段表示:
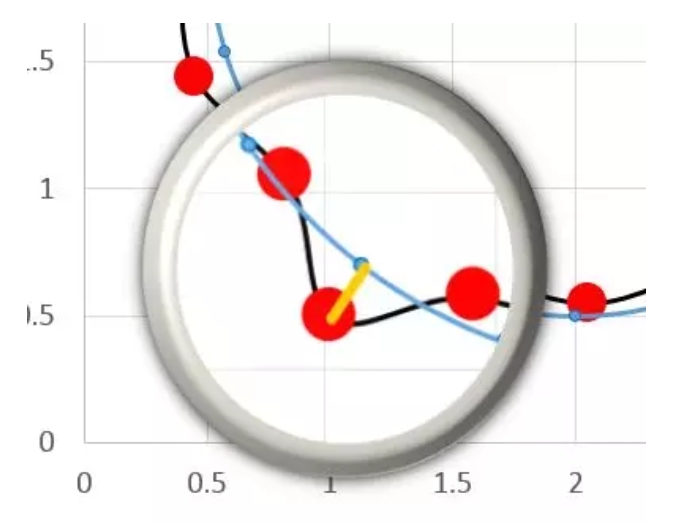
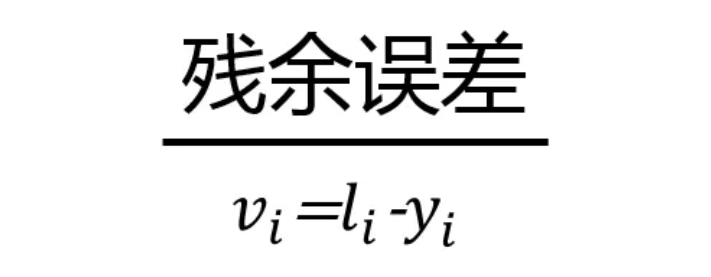
其中v表示殘余誤差,l表示實測點,y表示理想點。最理想的擬合圓應該能夠使所有測點殘余誤差平方和為最小,因此應該滿足如下表達式:
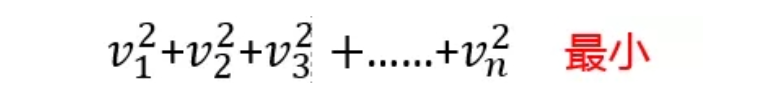
這就是最小二乘法。











 掃描關注我們
掃描關注我們